3
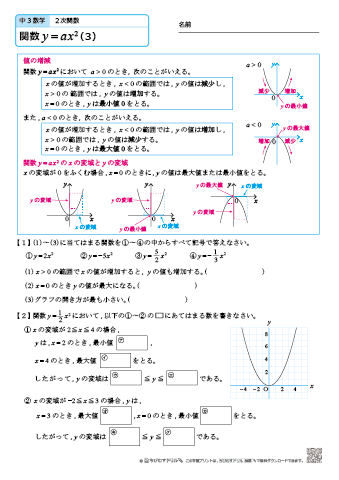
二次関数の問題では、その最大・最小を求める問題が出題されます。 つまり、二次関数について、xの範囲が問題において限定されます。 そのxの範囲内で、最大の値となるy、最小の値となるyをそれぞれ求める必要があるのです。 この問題を解く上では、どうしてもグラフの形状を考える必要がありますし、加えて、問題で指定されるxの範囲とグラフの関係がどのような位置関係にある この二次関数のグラフを書きましょう。 平方完成は、次の3つのポイントで行います。 逆に言えば、その3つのポイントさえおさえれば絶対に解けます。 定数項以外を()でくくる xの係数に注目して、それを2で割って2乗した数値を使う その数値を
二次関数 グラフ 問題 中学
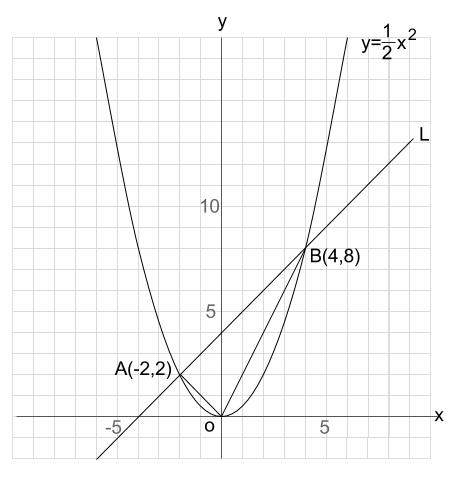
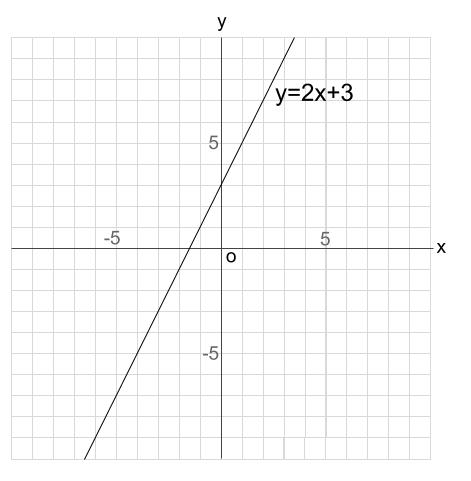
二次関数 グラフ 問題 中学- ズバリ、 一次関数と二次関数を組み合わせたグラフ です! で『一次関数と二次関数のグラフ』の問題では必ず 直線の式 が要求されます。 こんな感じの問題はよく出ますし苦手な生徒も多いですね^^;(新教研1月号過去問から) 中学数学の二次関数はこれです! y = ax2 y = a x 2 トムソン これが何かわからないよ そんな声が聞こえてきそうですね。 理解するために「そもそも関数って何? 」を簡単に説明します。 関数とはx x を入れたらy y が出てくる機械 関数とは、何か数字を x x として入れたら、何かの数字が y y として返ってくる機械のことです。 例えば y = 2x1 y = 2 x 1 という一次関数があったとしま
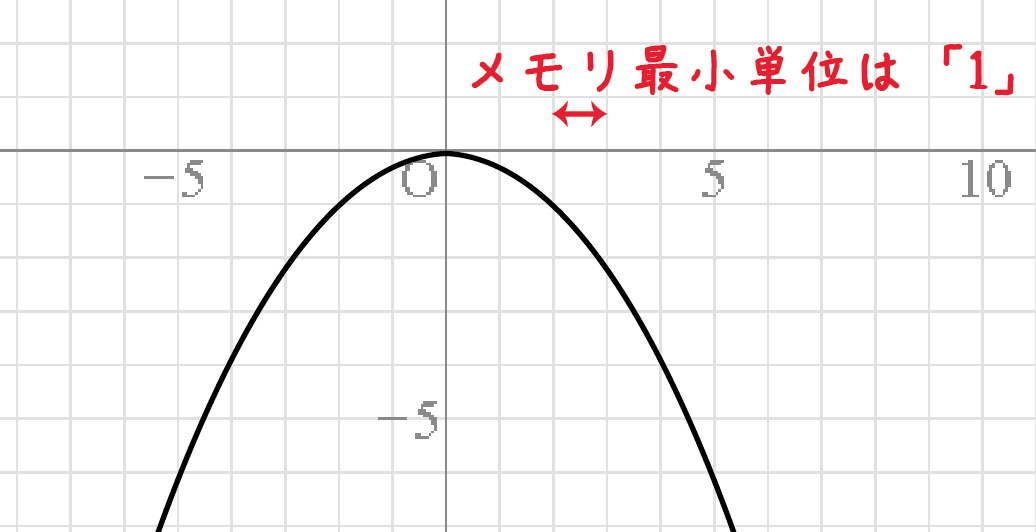
中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく
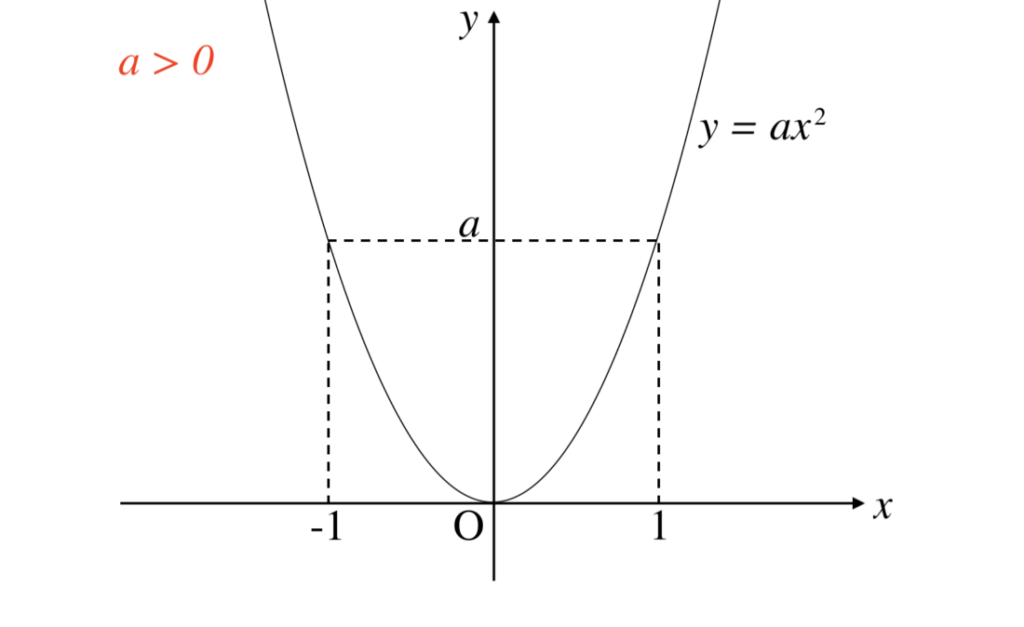
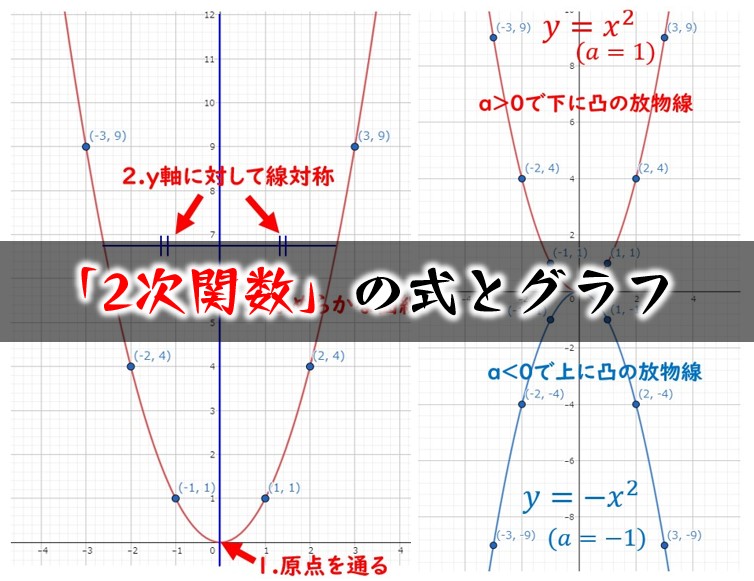
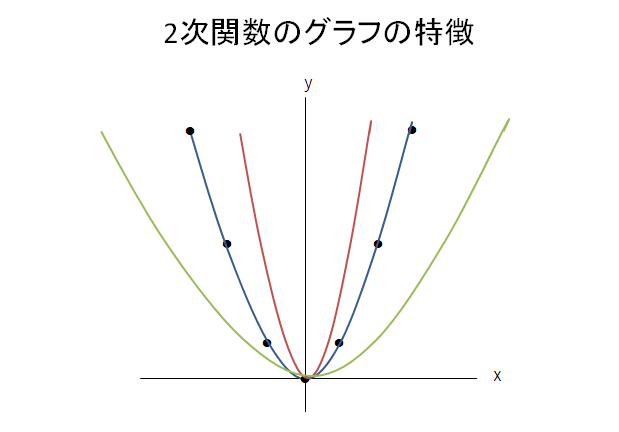
2次関数のグラフの特徴の練習問題の解答 二次関数のグラフの特徴のポイント 原点を通る(頂点は、原点である) y軸に対称 放物線になる a>0のとき、上に開く。 a<0のとき、下に開く。 aの絶対値が大きくなるほど、開きはせまくなる。 aの絶対値が等しく、符号がことなる2つのグラフの組は、x軸に対称。 二次関数のグラフここで差がつく たとえば、y=2x 2 のとき、 x<0の範囲では では問題です。 関数 y = 5x² y = 5 x ² について、以下の問いに答えましょう。 (1) x = 2 x = 2 のときの y y の値 (2) y = 2 y = 2 のときの x x の値 答えはこちらをクリック さらに問題です。 y y を x x の式で表しましょう。 また、それぞれについて、 x = −4動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru
FdData 中間期末:中学数学3 年:二次関数の応用 放物線の式・直線の式・交点など/面積を求める/面積の二等分/等積変形/ 線分比と面積比 /正方形・平行四辺形など/落下運動・制動距離など/動点/ 図形の移動による重なる面積/カテゴリ: @ y=ax^2(2次関数)のグラフ 高校入試 中学数学 関数 スポンサーリンク ロングコートダディ堂前透さんの出身地ということで福井県の問題を紹介していきますが,とてもとてもとても良問です。 解説するとき楽しそう。 難問だ関数 2乗に比例する関数1 2乗に比例する関数2 2乗に比例する関数3 2乗に比例する関数4 2乗に比例する関数5 2乗に比例する関数6 放物線と直線の変域が一致する 例題と練習 放物線と図形1 放物線と図形2 放物線と面積 相似 相似1 (基本問題) 相似2 (基本問題) 相似3 (基本問題) 三平方の定理
二次関数 グラフ 問題 中学のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
「二次関数 グラフ 問題 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「二次関数 グラフ 問題 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「二次関数 グラフ 問題 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「二次関数 グラフ 問題 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
「二次関数 グラフ 問題 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「二次関数 グラフ 問題 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「二次関数 グラフ 問題 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
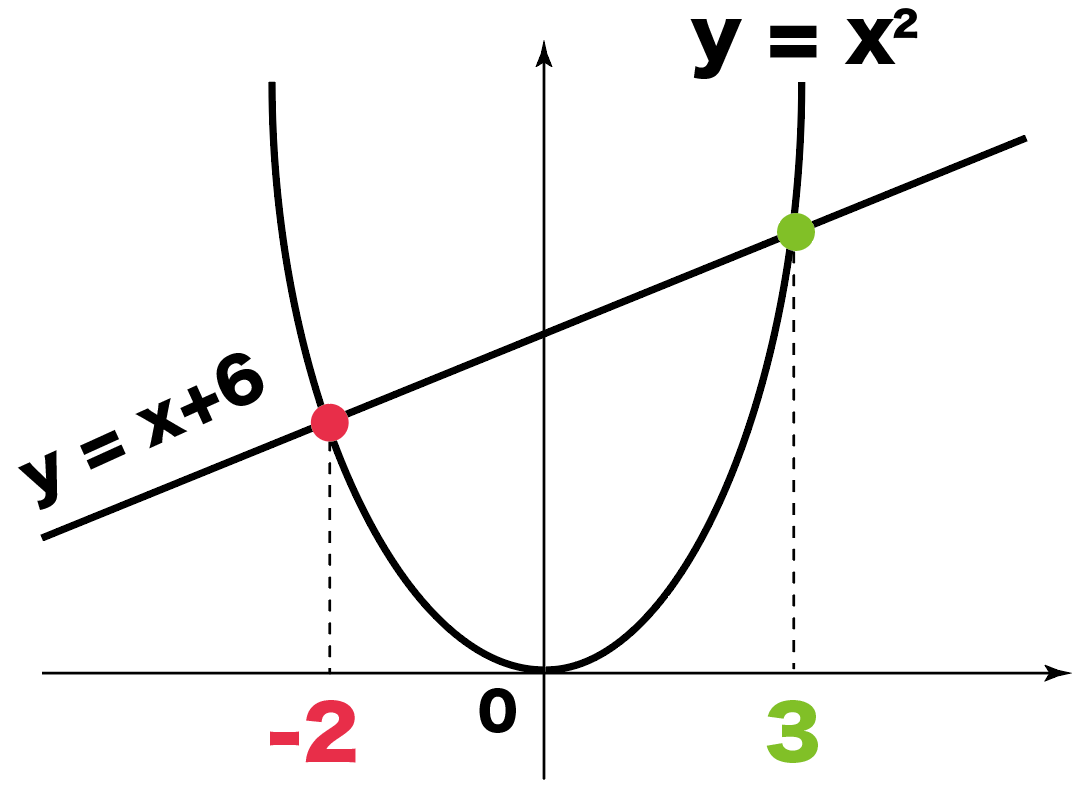 |  |  |
 |  |  |
「二次関数 グラフ 問題 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「二次関数 グラフ 問題 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「二次関数 グラフ 問題 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |
解答 二次関数 11 1 (1) において次の変化の割合を求めなさい 1.xが1から3まで増加 2.xがー4からー1まで増加 3.xがー2から3まで増加 1. 2. 3. ・においてxがbからcまで増加するとき 変化の割合 なので中学で習う二次関数の変化の割合は雑に表現するネットレ式中3数学 問NO 下の式をグラフに示せ。 (表を完成後、その座標を図に示す。 ) ★上の表の5つの座標を右のグラフ上でクリックし示しなさい。 ★5点選択後,線を引くボタンを押しなさい。 参加しますか?
Incoming Term: 二次関数 グラフ 問題 中学,




0 件のコメント:
コメントを投稿